Given:
Volume of a sphere is
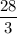 times the surface area.
times the surface area.
To find:
The surface area and the volume of the sphere.
Solution:
Volume of a sphere:
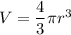 ...(i)
...(i)
Surface area of a sphere:
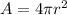 ...(ii)
...(ii)
Where, r is the radius of the sphere.
Volume of a sphere is
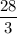 times the surface area.
times the surface area.
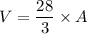
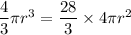
Multiply both sides by 3.
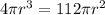
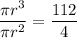
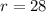
Using (i), the volume of the sphere is:
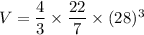
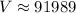
Using (ii), the surface area of the sphere is:
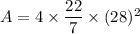
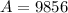
Therefore, the surface area of the sphere is 9856 sq. units and the volume of the sphere is 91989 cubic units.