Question

Question 6 plz show ALL STEPS

Answer 1

Explanation:

6a. Both the x and y coordinates are negative so this means isn't must be in the Third Quadrant.

6b. The measure of this using the unt circle is

`\cos(x) - (1)/(2)`

`\sin(x) = - ( √(3) )/(2)`

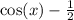
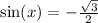
In the unit circle, this occurs about

an angle of 240 degrees. We can find coterminal angles within the interval of 2 pi to -2 pi. Just subtract 260 from theta.( which is 240)

`240 - 360 = - 120`

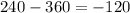
So the angles in the interval is

240, -120.

6c. pi/2 is the same as 90 degrees so this means that

`(240 + 90) = 330`

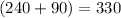
In the unit circle, we know that at 330 degrees,

`\cos(330) = ( √(3) )/(2)`

`\sin(330) = (1)/(2)`

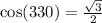
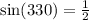
So the coordinates are

(sqr root of 3/2, 1/2).

6d. pi is the same as 180 degrees so this means that

`(240 - 180) = 60`

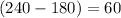
In the unit circle, we know that 60 degrees,

`\cos(60) = (1)/(2)`

`\sin(60) = ( √(3) )/(2)`

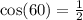
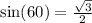
So the coordinates are

(1/2, sqr root of 3/2)