Answer:
(-5, 0) and (5, 0)
Explanation:
This equation fits the form for a hyperbola with x-intercepts. The standard form for such an equation is
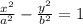
To get the equation in the question into this standard form, divide each term by 400.

To find the x-intercepts, make y = 0.
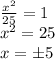
The vertices are located at the points (-5, 0) and (5, 0).
Note: There are no y-intercepts; making x = 0 produces no real solutions for y.