Question

Help with 1 b please. using ln.​

Answer 1

`\displaystyle (dy)/(dx) = \frac{1}{(x - 2)^2\sqrt{(x)/(2 - x)}}`

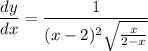
General Formulas and Concepts:

Pre-Algebra

• Equality Properties

Algebra I

• Terms/Coefficients
• Factoring
• Exponential Rule [Root Rewrite]:
  `\displaystyle \sqrt[n]{x} = x^{(1)/(n)}`

Algebra II

• Natural logarithms ln and Euler's number e
• Logarithmic Property [Exponential]:
  `\displaystyle log(a^b) = b \cdot log(a)`

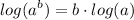
Calculus

Differentiation

• Derivatives
• Derivative Notation
• Implicit Differentiation

Derivative Property [Multiplied Constant]:
`\displaystyle (d)/(dx) [cf(x)] = c \cdot f'(x)`

Derivative Property [Addition/Subtraction]:
`\displaystyle (d)/(dx)[f(x) + g(x)] = (d)/(dx)[f(x)] + (d)/(dx)[g(x)]`

Basic Power Rule:

1. f(x) = cxⁿ
2. f’(x) = c·nxⁿ⁻¹

Derivative Rule [Quotient Rule]:
`\displaystyle (d)/(dx) [(f(x))/(g(x)) ]=(g(x)f'(x)-g'(x)f(x))/(g^2(x))`

Derivative Rule [Chain Rule]:
`\displaystyle (d)/(dx)[f(g(x))] =f'(g(x)) \cdot g'(x)`

Explanation:

*Note:

You can simply just use the Quotient and Chain Rule to find the derivative instead of using ln.

Step 1: Define

Identify

`\displaystyle y = \sqrt{(x)/(2 - x)}`

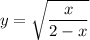
Step 2: Rewrite

1. [Function] Exponential Rule [Root Rewrite]:
   `\displaystyle y = \bigg( (x)/(2 - x) \bigg)^\bigg{(1)/(2)}`
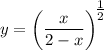
2. [Equality Property] ln both sides:
   `\displaystyle lny = ln \bigg[ \bigg( (x)/(2 - x) \bigg)^\bigg{(1)/(2)} \bigg]`
3. Logarithmic Property [Exponential]:
   `\displaystyle lny = (1)/(2)ln \bigg( (x)/(2 - x) \bigg)`

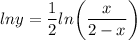
Step 3: Differentiate

1. Implicit Differentiation:
   `\displaystyle (dy)/(dx)[lny] = (dy)/(dx) \bigg[ (1)/(2)ln \bigg( (x)/(2 - x) \bigg) \bigg]`
2. Logarithmic Differentiation [Derivative Rule - Chain Rule]:
   `\displaystyle (1)/(y) \ (dy)/(dx) = (1)/(2) \bigg( (1)/((x)/(2 - x)) \bigg) (dy)/(dx) \bigg[ (x)/(2 - x) \bigg]`
3. Chain Rule [Basic Power Rule]:
   `\displaystyle (1)/(y) \ (dy)/(dx) = (1)/(2) \bigg( (1)/((x)/(2 - x)) \bigg) \bigg[ (2)/((x - 2)^2) \bigg]`
4. Simplify:
   `\displaystyle (1)/(y) \ (dy)/(dx) = (-1)/(x(x - 2))`
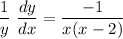
5. Isolate
   `\displaystyle (dy)/(dx)`:
   `\displaystyle (dy)/(dx) = (-y)/(x(x - 2))`
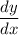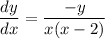
6. Substitute in y [Derivative]:
   `\displaystyle (dy)/(dx) = \frac{-\sqrt{(x)/(2 - x)}}{x(x - 2)}`
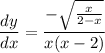
7. Rationalize:
   `\displaystyle (dy)/(dx) = \frac{-(x)/(2 - x)}{x(x - 2)\sqrt{(x)/(2 - x)}}`
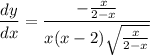
8. Rewrite:
   `\displaystyle (dy)/(dx) = \frac{-x}{x(x - 2)(2 - x)\sqrt{(x)/(2 - x)}}`
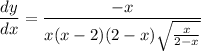
9. Factor:
   `\displaystyle (dy)/(dx) = \frac{-x}{-x(x - 2)^2\sqrt{(x)/(2 - x)}}`
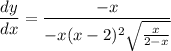
10. Simplify:
    `\displaystyle (dy)/(dx) = \frac{1}{(x - 2)^2\sqrt{(x)/(2 - x)}}`

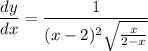
Topic: AP Calculus AB/BC (Calculus I/I + II)

Unit: Differentiation

Book: College Calculus 10e