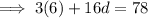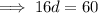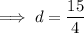Answer:
First term: 6
Common difference: 15/4
Explanation:
General form of arithmetic progression:
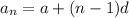
(where
 is the initial term and
is the initial term and
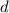 is the common difference between terms)
is the common difference between terms)
Question (a)
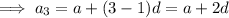
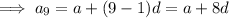
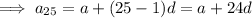
Question (b)
General form of a geometric progression:

(where
 is the initial term and
is the initial term and
 is the common ratio)
is the common ratio)
Therefore, the first three terms of a geometric series are:
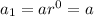
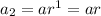
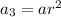
To find the common ratio:
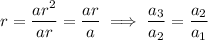
If the 3rd 9th and 25th terms of an arithmetic progression form the first three consecutive terms of a geometric series, then inputting these into the above formula for r:
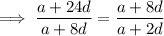
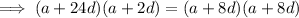
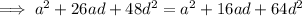
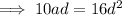
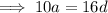
The 6th and 7th terms of the arithmetic progression are:
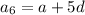
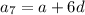
If the sum of the 7th and twice the 6th term of the arithmetic progression is 78, then:
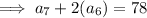
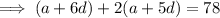
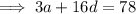
Substituting
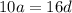 into
into
 and solving for a:
and solving for a:
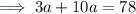
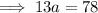
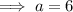
Substituting
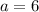 into
into
 and solving for d:
and solving for d: