Question

A triangle and a parallelogram have the same base and the same area.

If the sides of the triangle are 26 cm, 28 cm and 30 cm and the
parallelogram stands on the base 28 cm. Find the height of the
parallelogram.

Answer 1

12 centimeters

Explanation:

The side lengths of the triangle are: 26, 28, and 30 centimeters

a = 26 cm, b = 28 cm, c = 30 cm

To find the area, we first must find the semi-perimeter with the following equation:

s = (a+b+c)/2

= (28+26+30)/2

= 42 centimeters

Now, to find the area, we can use Heron's formula:

A =
`√(s (s-a)(s-b)(s-c))`

`\sqrt{42(42-28)(42-26)(42-30)`

`√(42(14)(16)(12))`

`√(112896)`

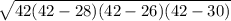
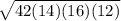
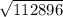
336 squared centimeters

Since the area of the parallelogram is equal to the area of our triangle:

Area of Parallelogram = Area of Triangle

base ⋅ height = 336 squared centimeters

28 ⋅ height = 336 squared centimeters

height = 336/28

height = 12 centimeters