Question

Find the arclength of the curve r(t) = ⟨ 10sqrt(2)t , e^(10t) , e^(−10t)⟩, 0≤t≤1

Answer 1

`\displaystyle AL = 2sinh(10)`

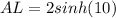
General Formulas and Concepts:

Pre-Calculus

• Hyperbolic Functions

Calculus

Differentiation

• Derivatives
• Derivative Notation

Derivative Property [Multiplied Constant]:
`\displaystyle (d)/(dx) [cf(x)] = c \cdot f'(x)`

Derivative Rule [Chain Rule]:
`\displaystyle (d)/(dx)[f(g(x))] =f'(g(x)) \cdot g'(x)`

Basic Power Rule:

1. f(x) = cxⁿ
2. f’(x) = c·nxⁿ⁻¹

Exponential Differentiation

Integration

• Integrals
• Integration Constant C
• Definite Integrals

Parametric Integration

Vector Value Functions

• Vector Integration

Arc Length Formula [Vector]:
`\displaystyle AL = \int\limits^b_a {√([i'(t)]^2 + [j'(t)]^2 + [k'(t)]^2)} \, dt`

Explanation:

Step 1: Define

Identify

`\displaystyle \vec{r}(t) = <10√(2)t , e^(10t) , e^(-10t) >`

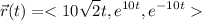
Interval [0, 1]

Step 2: Find Arclength

1. Rewrite vector value function:
   `\displaystyle r(t) = 10√(2)t \textbf i + e^(10t) \textbf j + e^(-10t) \textbf k`
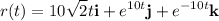
2. Substitute in variables [Arc Length Formula - Vector]:
   `\displaystyle AL = \int\limits^1_0 {\sqrt{\bigg[(d)/(dt)[10√(2)t \textbf i]\bigg]^2 + \bigg[(d)/(dt)[e^(10t) \textbf j]\bigg]^2 + \bigg[(d)/(dt)[e^(-10t) \textbf k ]\bigg]^2}} \, dt`
3. [Integrand] Differentiate [Respective Differentiation Rules]:
   `\displaystyle AL = \int\limits^1_0 {\sqrt{[10√(2) \textbf i]^2 + [10e^(10t) \textbf j]^2 + [-10e^(-10t) \textbf k]^2}} \, dt`
4. [Integrand] Simplify:
   `\displaystyle AL = \int\limits^1_0 {\sqrt{200 \textbf i + 100e^(20x) \textbf j + 100e^(-20x) \textbf k}} \, dt`
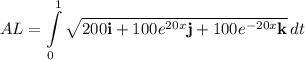
5. [Integral] Evaluate:
   `\displaystyle AL = 2sinh(10)`

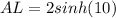
Topic: AP Calculus BC (Calculus I + II)

Unit: Vector Value Functions

Book: College Calculus 10e