Question

A toy rocket is shot vertically into the air from a launching pad 9 feet above the ground with an initial velocity of 88 feet per second. The height h, in feet, of the rocket above the ground at t seconds after launch is given by the function

h(t) - 16^2 + 88ft +9. How long will it take the rocket to reach its maximum height? What is the maximum height?
The rocket reaches its maximum height at ____ second(s) after launch.
(Simplify your answer.)

Answer 1

Explanation:

The position function for this is:

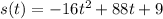`s(t)=-16t^2+88t+9`. We can use this equation to find the position (or height) of the rocket at ANY TIME during its flight. I could find out the height of the rocket at 3 seconds by plugging in a 3 for t and solving for s(t); I could find the height of the rocket at 12 seconds by plugging in a 12 for t and solving for s(t), etc.

The first derivative of position is velocity:

v(t) = -32t + 88.

If we are looking for the time the rocket reaches it max height, we need to remember from physics class that this happens when the velocity of the object is at 0. We set the velocity equation equal to 0 then and solve for t:

0 = -32t + 88 and

-88 = -32t so

t = 2.75 seconds. This means that 2.75 seconds after the rocket is launched, it reaches its max height. In order to find what that max height is we plug 2.75 into the position equation for t and solve:

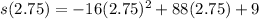`s(2.75)=-16(2.75)^2+88(2.75)+9` to get that

s(2.75) = 130

The max height is 130 feet and it reaches this point at 2.75 seconds into its motion.