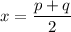Question

6. If the zeros of a quadratic funtion, f(x), are -2 and 6, what is the equation of the axis of

symmetry of f(x)?
ints
a. X= -2
b. X= 2
c. X= 4
d. Cannot be determined

Answer 1

B

Explanation:

We are given a quadratic function f(x) whose zeros are at x = -2 and x = 6.

And we want to determine its axis of symmetry.

Recall that a parabola is symmetric about its axis of symmetry.

Therefore, the axis of symmetry is directly in the middle of the two roots.

Find the average of the roots:

`\displaystyle x=((-2)+(6))/(2)=(4)/(2)=2`

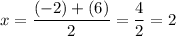
Hence, the axis of symmetry is x = 2.

Our answer is B.

In general, if we are given the two zeros p and q of a quadratic and we want to find the axis of symmetry x, it is given by:

`\displaystyle x = (p+q)/(2)`