Answer:
Josh's ERA had a z-score of -3.26.
Alice's ERA had a z-score of -1.11.
Due to the lower z-score(ERA is a stat that the lower the better), Josh had a better year relative to his peers.
Explanation:
Z-score:
In a set with mean
 and standard deviation
and standard deviation
 , the z-score of a measure X is given by:
, the z-score of a measure X is given by:

The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the p-value, we get the probability that the value of the measure is greater than X.
Josh:
ERA of 2.89, mean of 5.083, standard deviation of 0.672. So
 , and the z-score is:
, and the z-score is:

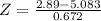

Josh's ERA had a z-score of -3.26.
Alice:
ERA of 3.31, mean of 4.032, standard deviation of 0.649. So
 , and the z-score is:
, and the z-score is:

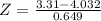

Alice's ERA had a z-score of -1.11.
Which player had the better year relative to their peers, josh or alice ?
Due to the lower z-score(ERA is a stat that the lower the better), Josh had a better year relative to his peers.