Answer:
Fourth option
Explanation:
If you dont have a graphing calculator, we can solve this system using elimination. If we subtract the two linesr functions, we get
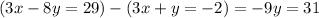
So our new equation is
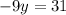
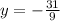
Now since we know what y is, we plug this in back into the equation and solve for x.
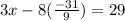
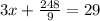
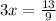
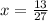
The answer choice that resembles this mostly is the fourth option.