Question

The average electric bill for a small electric company is $72 for the month of April with a standard deviation of $6. If the amounts of the bills are normally distributed, find the probability that the mean of the bills for 15 randomly selected residents will be less than $75

Answer 1

Hence the probability that the mean of their utility bills will be less than $75 = P(X < 75) is 0.9736.

Explanation:

Now,

Population mean electric bill,
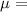`\mu =` $72

Population standard deviation,
`\sigma =` $6

Standard error of the mean
`= \sigma / √(n) = 6 / √(15) = 1.5492`

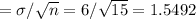
The probability that the mean of their utility bills will be less than $75 = P(X < 75)

= P[Z < (75 - 72) / 1.5492]

= P[Z < 1.9365]

= 0.9736 (Using Z table)