Question

A county office gets an average of 10 calls in a 2 hour time period. What is the probability that the county office will get more than 0 calls in a 15 minute period? Round your answer to three decimal places.

Answer 1

0.713 = 71.3% probability that the county office will get more than 0 calls in a 15 minute period.

Explanation:

We have the mean during a time-period, which means that the Poisson distribution is used to solve this question.

In a Poisson distribution, the probability that X represents the number of successes of a random variable is given by the following formula:

`P(X = x) = (e^(-\mu)*\mu^(x))/((x)!)`

In which

x is the number of sucesses

e = 2.71828 is the Euler number

`\mu` is the mean in the given interval.

A county office gets an average of 10 calls in a 2 hour time period.

10 calls each 120 minutes, which means that the mean for n minutes is:

`\mu = (10n)/(120) = (n)/(12)`

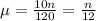
15 minute period:

This means that
`n = 15, \mu = (15)/(12) = 1.25`

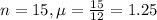
What is the probability that the county office will get more than 0 calls in a 15 minute period?

This is:

`P(X > 0) = 1 - P(X = 0)`

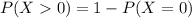
In which

`P(X = x) = (e^(-\mu)*\mu^(x))/((x)!)`

`P(X = 0) = (e^(-1.25)*1.25^(0))/((0)!) = 0.287`

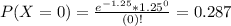
So

`P(X > 0) = 1 - P(X = 0) = 1 - 0.287 = 0.713`

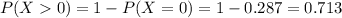
0.713 = 71.3% probability that the county office will get more than 0 calls in a 15 minute period.