Answer:

Explanation:
Hi there!
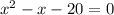
This equation is written in the form
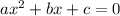 . First, use partial factoring:
. First, use partial factoring:

For x^2-x, the b value is -1 in
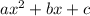 . To complete the square, take the square of half of 1 and add it in the parentheses as the c value:
. To complete the square, take the square of half of 1 and add it in the parentheses as the c value:
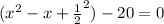
However, when adding values to one side of the equation, we must to the same to the other side:

Complete the square:

Move 20 to the other side
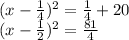
I hope this helps!