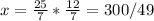Answer:
A proportion equation is something like:
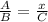
Where A, B, and C are known numbers, and we want to find the value of x.
Now we want two cases where in one of the numerators we have a mixed number, where a mixed number is something like:
1 and 1/3
which actually should be written as:
1 + 1/3
1) a random problem can be:
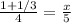
We can see that the numerator on the left is a mixed number.
First, let's rewrite the numerator then:
1 + 1/3
we need to have the same denominator in both numbers, so we can multiply and divide by 3 the number 1:
(3/3)*1 + 1/3
3/3 + 1/3 = 4/3
now we can rewrite our equation as:
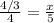
now we can solve this:
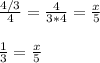
now we can multiply both sides by 5 to get:
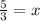
Now let's look at another example, this time we will have the variable x in the denominator:
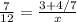
We can see that we have a mixed number in one numerator.
Let's rewrite that number as a fraction:
3 + 4/7
let's multiply and divide the 3 by 7.
(7/7)*3 + 4/7
21/7 + 4/7
25/7
Then we can rewrite our equation as
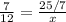
Now we can multiply both sides by x to get:
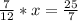
Now we need to multiply both sides by (12/7) to get: