Answer:
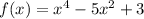 is symmetric to the y-axis
is symmetric to the y-axis
Explanation:
Given
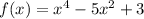
Required
Determine if it is symmetric
First, we check if the function is even by calculating f(-x)
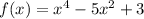
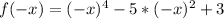
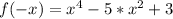
We have:
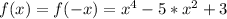
This implies that the function is even, and even functions are symmetric to the y-axis.
Hence:
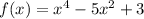 is symmetric to the y-axis
is symmetric to the y-axis