Answer:
The absolute value of the quadratic term,
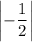 is less than 1
is less than 1
Explanation:
The given function is y = (-1/2)·x² - 7
The parent function is y = x²
The vertical compression or stretching of a quadratic function is given by the value of the coefficient, a, of the quadratic term, x² of a quadratic function, a·x²
A quadratic function is vertically compressed if the coefficient,
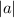 < 1.
< 1.
In the given function, y = (-1/2)·x² - 7, the absolute value of the coefficient of the quadratic term,
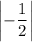 < 1, therefore, the equation, y = (-1/2)·x² - 7, will be vertically compressed compared to the parent function, y = x².
< 1, therefore, the equation, y = (-1/2)·x² - 7, will be vertically compressed compared to the parent function, y = x².