Question

Find the value of a for which there is no term independent of x in the ezlxpansion of


`(1 + ax {}^(2) )( (2)/(x) - 3x) {}^(6)`
​

Answer 1

"no terms independent of x" basically means there is no constant term, or the coefficient of x ⁰ is zero.

Recall the binomial theorem:

`\displaystyle (a+b)^n=\sum_(k=0)^n\binom nk a^(n-k)b^k`

So we have

`\displaystyle \left(1+ax^2\right)\left(\frac2x-3x\right)^6 = \left(1+ax^2\right) \sum_(k=0)^6 \binom 6k \left(\frac2x\right)^(6-k)(-3x)^k`

`\displaystyle \left(1+ax^2\right)\left(\frac2x-3x\right)^6 = \left(1+ax^2\right) \sum_(k=0)^6 2^(6-k)(-3)^k\binom 6k x^(2k-6)`

`\displaystyle \left(1+ax^2\right)\left(\frac2x-3x\right)^6 = \sum_(k=0)^6 2^(6-k)(-3)^k\binom 6k x^(2k-6)+a\sum_(k=0)^6 2^(6-k)(-3)^k\binom 6k x^(2k-4)`

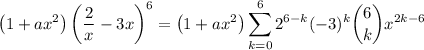
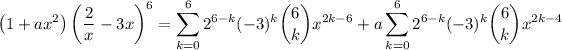
The first sum contributes a x ⁰ term for 2k - 6 = 0, or k = 3, while the second sum contributes a x ⁰ term for 2k - 4 = 0, or k = 2. The coefficient of the sum of these terms must be zero:

`2^(6-3)(-3)^3\dbinom 63 + a*2^(6-2)(-3)^2\dbinom 62 = 0`

which reduces to

2160a - 4320 = 0

2160a = 4320

a = 2