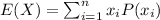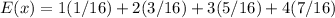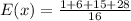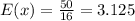Question

You throw two four-sided dice. Let the random variable X represent the maximum value of the two dice. Compute E(X). Round your answer to three decimal places.

Answer 1

E(X)=3.125

Explanation:

We are given that two four sided dice.

Then , the sample space

{(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4),(3,1),(3,2),(3,3),(3,4),(4,1),(4,2),(4,3),(4,4)}

Total number of outcomes=16

Let the random variable X represent the maximum value of the two dice

Outcomes X P(X)

(1,1) 1 1/16

(1,2),(2,1),(2,2) 2 3/16

(1,3),(2,3),(3,1),(3,2),(3,3) 3 5/16

(1,4),(3,4) ,(2,4),(4,1),(4,2),(4,3),(4,4) 4 7/16

Using the probability formula

`P(E)=(Favorable\;outcomes)/(Total\;number\;of\;outcomes)`

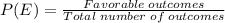
Now,

`E(X)=\sum_(i=1)^(n)x_iP(x_i)`

`E(x)=1(1/16)+2(3/16)+3(5/16)+4(7/16)`

`E(x)=(1+6+15+28)/(16)`

`E(x)=(50)/(16)=3.125`