Question

A freshly inoculated bacterial culture of Streptococcus contains 100 cells. When the culture is checked 60 minutes later, it is determined that there are 450 cells present. Assuming exponential growth, determine the number of cells present at any time t (measured in minutes) and the find the doubling time.​

Answer 1

`P(t) = 100e^(0.0251t)`

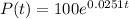
The doubling time is of 27.65 minutes.

Explanation:

Exponential equation of growth:

The exponential equation for population growth is given by:

`P(t) = P(0)e^(kt)`

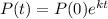
In which P(0) is the initial value and k is the growth rate.

A freshly inoculated bacterial culture of Streptococcus contains 100 cells.

This means that
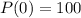`P(0) = 100`. So

`P(t) = 100e^(kt)`

When the culture is checked 60 minutes later, it is determined that there are 450 cells present.

This means that
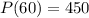`P(60) = 450`, and we use this to find k. So

`450 = 100e^(60k)`

`e^(60k) = 4.5`

`\ln{e^(60k)} = ln(4.5)`

`60k = ln(4.5)`

`k = (ln(4.5))/(60)`

`k = 0.0251`

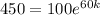
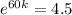
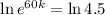
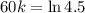
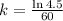
So

`P(t) = 100e^(0.0251t)`

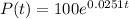
Doubling time:

This is t for which P(t) = 2P(0) = 200. So

`200 = 100e^(0.0251t)`

`e^(0.0251t) = 2`

`\ln{e^(0.0251t)} = ln(2)`

`0.0251t = ln(2)`

`t = (ln(2))/(0.0251)`

`t = 27.65`

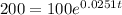
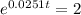
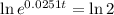
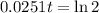
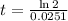
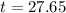
The doubling time is of 27.65 minutes.