Answer:
D. As the sample size is appropriately large, the margin of error is ±0.15
Explanation:
The number of students in the sample, n = 32 students
The percentage of the students that preferred studying abroad,
 = 25%
= 25%
The confidence level for the study = 95%
As a general rule, a sample size of 30 and above are taken as sufficient
The z-value at 95% confidence level, z = 1.96
The margin of error of a proportion formula is given as follows;
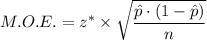
Therefore, we get;
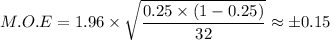
Therefore, the correct option is that as the sample size is appropriately large, the margin of error is ±0.15.