Answer:
325
Explanation:
You must have heard about Arithmetic Progressions (AP)
Arithmetic progressions are a series of numbers such that every successive number is the sum of a constant number and the previous number.
Our very own counting numbers form AP
For example :-
2 = 1 + 1
3 = 2 + 1
4 = 3 + 1
The number in bold (1) is that constant number which is added to a number to form its successive number.
To find the sum of series forming AP, we use the formula :-
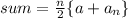
here,
- n is the number of terms
- a is the first number of the series
- an is the last number of the series
So we'll use all this information to find the sum of continuous numbers from 1 to 25 where 1 is the first term(a) and 25 is the last(an).
and n is 25
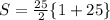
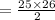
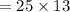
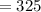
So, the value of S comes out to be 325.