Answer:
0.5555 = 55.55% probability of rolling a sum that is a multiple of 3 or a multiple of 4.
Explanation:
A probability is the number of desired outcomes divided by the number of total outcomes.
Possible outcomes:
For the pair of dice:
(1,1), (1,2), (1,3), (1,4), (1,5), (1,6)
(2,1), (2,2), (2,3), (2,4), (2,5), (2,6)
(3,1), (3,2), (3,3), (3,4), (3,5), (3,6)
(4,1), (4,2), (4,3), (4,4), (4,5), (4,6)
(5,1), (5,2), (5,3), (5,4), (5,5), (5,6)
(6,1), (6,2), (6,3), (6,4), (6,5), (6,6)
So 36 total outcomes.
Desired outcomes:
Sum being multiplies of 3 or multiples of 4, so:
(1,2), (1,3), (1,5)
(2,1), (2,2), (2,4), (2,6)
(3,1), (3,3), (3,5), (3,6)
(4,2), (4,4), (4,5)
(5,1), (5,3), (5,4)
(6,2), (6,3), (6,6)
3 + 4 + 4 + 3 + 3 + 3 = 20
Probability:
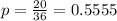
0.5555 = 55.55% probability of rolling a sum that is a multiple of 3 or a multiple of 4.