The graph of the functions y =
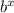 and
and
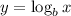 sketched and shown in
sketched and shown in
in the below picture.
The inverse of the logarithmic function
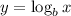 is y =
is y =
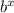 .
.
Plotted points on the graph are (1,0), (2, 1), (4, 2), (8, 3), and (16, 4), and they correspond to the function.
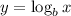
The graph of y = bx must have the following coordinates in order to determine the coordinates of the function.
Coordinate of
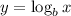
Coordinate of y =
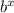
From the above graph, it is observed that the black curve represents the function y =
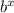 , and the green curve represents the function
, and the green curve represents the function
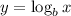
where as the coordinates of the graph of the functions y =
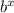 and
and
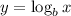 connected by the smooth curve.
connected by the smooth curve.