Question

Water exits straight down from a faucet with a 1.96-cm diameter at a speed of 0.55 m/s. The volume flow rate of the water as it exits from the faucet is Blank

1. Calculate the answer by read surrounding text. cm3/s. As the water falls from the faucet with the given speed, it accelerates due to gravity and reaches a speed of _______
2. Calculate the answer by read surrounding text. after it has moved 0.2 m downward. With this change in speed of the water, the diameter of the stream 0.2 m below the faucet is _______
3. Calculate the answer by read surrounding text. _________ cm.

Answer 1

Q = 165.95 cm³ / s, 1) v =
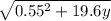`√(0.55^2 + 19.6 y)`, 2) v = 2.05 m / s,

3) d₂ = 1.014 cm

Step-by-step explanation:

This is a fluid mechanics exercise

1) the continuity equation is

Q = v A

where Q is the flow rate, A is area and v is the velocity

the area of ​​a circle is

A = π r²

radius and diameter are related

r = d / 2

substituting

A = π d²/4

Q = π/4 v d²

let's reduce the magnitudes

v = 0.55 m / s = 55 cm / s

let's calculate

Q = π/4 55 1.96²

Q = 165.95 cm³ / s

If we focus on a water particle and apply the zimematics equations

v² = v₀² + 2 g y

where the initial velocity is v₀ = 0.55 m / s

v =
`√(0.55^2 + 2 \ 9.8\ y)`

v =
`√(0.55^2 + 19.6 y)`

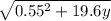
2) ask to calculate the velocity for y = 0.2 m

v =
`√(0.55^2 + 19.6 \ 0.2)`

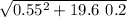
v = 2.05 m / s

3) We write the continuous equation for this point 2

Q = v₂ A₂

A₂ = Q / v₂

let us reduce to the same units of the SI system

Q = 165.95 cm³ s (1 m / 10² cm) ³ = 165.95 10⁻⁶ m³ / s

A₂ = 165.95 10⁻⁶ / 2.05

A₂ = 80,759 10⁻⁶ m²

area is

A₂ = π/4 d₂²

d₂ =
`√(4 A_2 / \pi )`

d₂ =
`\sqrt{ (4 \ 80.759 \ 10^(-6) )/(\pi ) }`

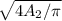
d₂ = 10.14 10⁻³ m

d₂ = 1.014 cm