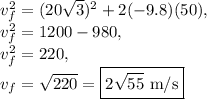Question

A particle is projected with a velocity of
`40ms^-^1` at an elevation of 60°. Calculate the vertical component of its velocity at a height of 50m. (Take g =
`9.8ms^-^2`)

A.
`25√(3) ms^-^1\\\\B.20√(3) ms^-^1\\\\c. 2√(545) ms^-^1`

Answer 1

`2√(55)\text{ m/s or }\approx 14.8\text{m/s}`

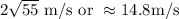
Explanation:

The vertical component of the initial launch can be found using basic trigonometry. In any right triangle, the sine of an angle is equal to its opposite side divided by the hypotenuse. Let the vertical component at launch be
`y`. The magnitude of
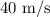`40\text{ m/s}` will be the hypotenuse, and the relevant angle is the angle to the horizontal at launch. Since we're given that the angle of elevation is
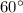`60^(\circ)`, we have:

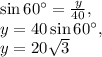`\sin 60^(\circ)=(y)/(40),\\y=40\sin 60^(\circ),\\y=20√(3)`(Recall that
`\sin 60^(\circ)=(√(3))/(2)`)

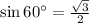Now that we've found the vertical component of the velocity and launch, we can use kinematics equation
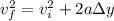`v_f^2=v_i^2+2a\Delta y` to solve this problem, where
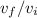`v_f/v_i` is final and initial velocity, respectively,
`a` is acceleration, and
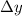`\Delta y` is distance travelled. The only acceleration is acceleration due to gravity, which is approximately
`9.8\:\mathrm{m/s^2}`. However, since the projectile is moving up and gravity is pulling down, acceleration should be negative, represent the direction of the acceleration.

What we know:

• 
  `v_i=20√(3)\text{ m/s}`
• 
  `a=-9.8\:\mathrm{m/s^2}`
• 
  `\Delta y =50\text{ m}`

Solving for
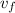`v_f`:

`v_f^2=(20√(3))^2+2(-9.8)(50),\\v_f^2=1200-980,\\v_f^2=220,\\v_f=√(220)=\boxed{2√(55)\text{ m/s}}`