Answer:
1,404,000 unique passwords are possible.
Explanation:
The order in which the letters and the digits are is important(AB is a different password than BA), which means that the permutations formula is used to solve this question.
Permutations formula:
The number of possible permutations of x elements from a set of n elements is given by the following formula:
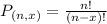
In this question:
2 digits from a set of 10(there are 10 possible digits, 0-9).
3 characters from a set of 26. So
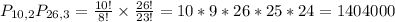
1,404,000 unique passwords are possible.