The object's kinetic energy changes according to
dK/dt = 15 J/s
If v is the object's initial speed, then its initial kinetic energy is
K (0) = 1/2 (5 kg) v ²
Use the fundamental theorem of calculus to solve for K as a function of time t :
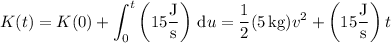
After t = 13 s, the object's kinetic energy is
K (13 s) = 1/2 (5 kg) (13 m/s)² = 422.5 J
Put this as the left side in the equation above for K(t) and solve for v :
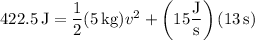
==> v ≈ 9.5 m/s