Question

How many bit strings of length 10 do not contain the substring 00? In other words, how many strings of length 10, consisting only of 1 and 0, in which there are no two consecutive zeros?

(In response, write down only the number without spaces.)

Answer 1

144

Explanation:

For a bitstring of length n, there are Fibonacci(n+2) strings containing no two consecutive zeros. This can be seen by constructing the strings starting with n=1.

1-bit strings: 1, 0 -- 2 strings not containing consecutive 0s

2-bit strings: 11, 10, 01 -- 3 strings not containing consecutive 0s

Note that we have added 1 to all the 1-bit strings, and added 0 only to the string ending in 1.

3-bit strings: 111, 110, 101, 011, 010 -- 5 strings not containing consecutive 0s

Note that these 5 strings consist of all (3) of the 2-bit strings with 1 appended, and all (1) of the 2-bit strings ending in 1 with 0 appended. The number that now end in 0 is the number previously ending in 1.

__

If (x, y) represents the numbers of n-bit strings ending in (0, 1), then the number of (n+1)-bit strings ending in (0, 1) is (y, x+y). That is, the recursive relation is ...

`(x_1,y_1)=(1,1)\\(x_n,y_n)=(y_(n-1),\,x_(n-1)+y_(n-1))\\b_n=x_n+y_n\quad\text{number of n-bit strings without consecutive 0s}`

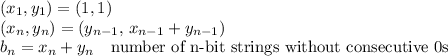
For n=1 to n=10, these pairs are ...

(1, 1), (1, 2), (2, 3), (3, 5), (5, 8), (8, 13), (13, 21), (21, 34), (34, 55), (55, 89)

The sequence of b[n] values is ...

2, 3, 5, 8, 13, 21, 34, 55, 89, 144

which are the n=3 to n=12 numbers from the Fibonacci sequence.

That is, there will be Fibonacci(12) = 144 10-bit strings with no consecutive 0s.