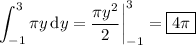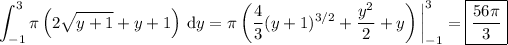Cross sections of the volume are washers or annuli with outer radii x(y) + 1, where
y = x(y) ² - 1 ==> x(y) = √(y + 1)
and inner radii 1. The distance between the outermost edge of each shell to the axis of revolution is then 1 + √(y + 1), and the distance between the innermost edge of R on the y-axis to the axis of revolution is 1.
For each value of y in the interval [-1, 3], the corresponding cross section has an area of
π (1 + √(y + 1))² - π (1)² = π (2√(y + 1) + y + 1)
Then the volume of the solid is the integral of this area over [-1, 3]: