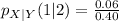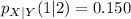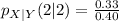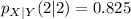Question

A service station has both self-service and full-service islands. On each island, there is a single regular unleaded pump with two hoses. Let X denote the number of hoses being used on the self-service island at a particular time, and let Y denote the number of hoses on the full-service island in use at that time. The joint pmf of X and Y appears in the accompanying tabulation.

p(x, y) y
0 1 2
x 0 0.10 0.03 0.01
1 0 08 0.20 0.06
2 0.05 0.14 0.33
(a) Given that X = 1, determine the conditional pmf of Y�i.e., pY|X(0|1), pY|X(1|1), pY|X(2|1).
(b) Given that two hoses are in use at the self-service island, what is the conditional pmf of the number of hoses in use on the full-service island?
(c) Use the result of part (b) to calculate the conditional probability P(Y ? 1 | X = 2).
(d) Given that two hoses are in use at the full-service island, what is the conditional pmf of the number in use at the self-service island?

Answer 1

(a): The conditional pmf of Y when X = 1

`p_(Y|X)(0|1) = 0.2353`

`p_(Y|X)(1|1) = 0.5882`

`p_(Y|X)(2|1) = 0.1765`

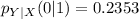
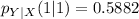
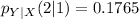
(b): The conditional pmf of Y when X = 2

`p_(Y|X)(0|2) = 0.0962`

`p_(Y|X)(1|2) = 0.2692`

`p_(Y|X)(2|2) = 0.6346`

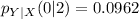
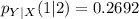
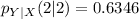
(c): From (b) calculate P(Y<=1 | X =2)

`P(Y\le1 | X =2) = 0.3654`

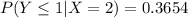
(d): The conditional pmf of X when Y = 2

`p_(X|Y)(0|2) = 0.025`

`p_(X|Y)(1|2) = 0.150`

`p_(X|Y)(2|2) = 0.825`

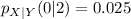
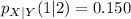
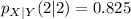
Explanation:

Given

The above table

Solving (a): The conditional pmf of Y when X = 1

This implies that we calculate

`p_(Y|X)(0|1), p_(Y|X)(1|1), p_(Y|X)(2|1)`

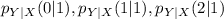
So, we have:

`p_(Y|X)(0|1) = (p(y = 0\ n\ x = 1))/(p(x = 1))`

Reading the data from the given table, the equation becomes

`p_(Y|X)(0|1) = (0.08)/(0.08+0.20+0.06)`

`p_(Y|X)(0|1) = (0.08)/(0.34)`

`p_(Y|X)(0|1) = 0.2353`

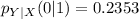
Using the format of the above formula for the rest, we have:

`p_(Y|X)(1|1) = (0.20)/(0.34)`

`p_(Y|X)(1|1) = 0.5882`

`p_(Y|X)(2|1) = (0.06)/(0.34)`

`p_(Y|X)(2|1) = 0.1765`

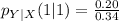
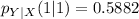
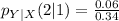
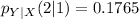
Solving (b): The conditional pmf of Y when X = 2

This implies that we calculate

`p_(Y|X)(0|2), p_(Y|X)(1|2), p_(Y|X)(2|2)`

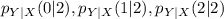
So, we have:

`p_(Y|X)(0|2) = (p(y = 0\ n\ x = 2))/(p(x = 2))`

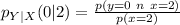
Reading the data from the given table, the equation becomes

`p_(Y|X)(0|2) = (0.05)/(0.05+0.14+0.33)`

`p_(Y|X)(0|2) = (0.05)/(0.52)`

`p_(Y|X)(0|2) = 0.0962`

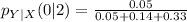
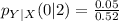
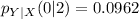
Using the format of the above formula for the rest, we have:

`p_(Y|X)(1|2) = (0.14)/(0.52)`

`p_(Y|X)(1|2) = 0.2692`

`p_(Y|X)(2|2) = (0.33)/(0.52)`

`p_(Y|X)(2|2) = 0.6346`

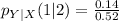
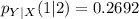
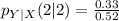
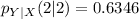
Solving (c): From (b) calculate P(Y<=1 | X =2)

To do this, where Y = 0 or 1

So, we have:

`P(Y\le1 | X =2) = P_(Y|X)(0|2) + P_(Y|X)(1|2)`

`P(Y\le1 | X =2) = 0.0962 + 0.2692`

`P(Y\le1 | X =2) = 0.3654`

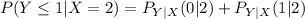
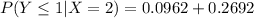
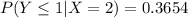
Solving (d): The conditional pmf of X when Y = 2

This implies that we calculate

`p_(X|Y)(0|2), p_(X|Y)(1|2), p_(X|Y)(2|2)`

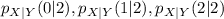
So, we have:

`p_(X|Y)(0|2) = (p(x = 0\ n\ y = 2))/(p(y = 2))`

Reading the data from the given table, the equation becomes

`p_(X|Y)(0|2) = (0.01)/(0.01+0.06+0.33)`

`p_(X|Y)(0|2) = (0.01)/(0.40)`

`p_(X|Y)(0|2) = 0.025`

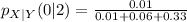
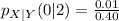
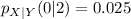
Using the format of the above formula for the rest, we have:

`p_(X|Y)(1|2) = (0.06)/(0.40)`

`p_(X|Y)(1|2) = 0.150`

`p_(X|Y)(2|2) = (0.33)/(0.40)`

`p_(X|Y)(2|2) = 0.825`