Question

A square pyramid is inscribed in a rectangular prism. A cone is inscribed in a cylinder. The pyramid and the cone have the same volume. Part of the volume of the rectangular prism, 1 V 1 , is not taken up by the square pyramid. Part of the volume of the cylinder, 2 V 2 , is not taken up by the cone. What is the relationship of these two volumes, 1 V 1 and 2 V 2 ?

Answer 1

V₂ = V₁

Explanation:

Let the height of the rectangular prism = h

Let s represent the side length of the base of the square prism, we have;

The volume of the prism,
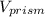`V_(prism)` = s²·h

The volume of the square pyramid,
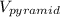`V_(pyramid)` = (1/3)·s²·h

∴ V₁ = The area not taken up by the square pyramid =
`V_(prism)` -
`V_(pyramid)`

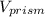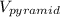
∴ V₁ = s²·h - (1/3)·s²·h = (2/3)·s²·h

Similarly, for the cylinder, we have;

Let h represent the height of the cylinder

Let r represent the radius of the base of the cone, we have;

Therefore;

The volume of the cylinder,
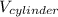`V_(cylinder)` = π·r²·h

The volume of the cone,
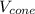`V_(cone)` = (1/3)·π·r²·h

∴ V₂ = π·r²·h - (1/3)·π·r²·h = (2/3)·π·r²·h

V₂ = (2/3)·π·r²·h

`V_(cone)` =
`V_(pyramid)`

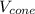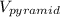
Therefore;

(1/3)·π·r²·h = (1/3)·s²·h

∴ π·r² = s²

Therefore, V₂ = (2/3)·π·r²·h = V₂ = (2/3)·s²·h = V₁

V₂ = V₁.