Question

Solve this quadratic equation by completing the square

x^2=12x+17

Answer 1

`\large\boxed{\red{\sf x =6+√(53),6-√(53)} }`

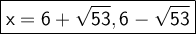
Explanation:

We would like to solve the given quadratic equation by completing the square method .The given equation is ;

`\longrightarrow x^2=12x +17`

Subtract 12x to both sides ,

`\longrightarrow x^2-12x = 17`

Here the co-efficient of x² is already 1 . So , we shall rewrite it as ,

`\longrightarrow x^2-2(6)(x) = 17`

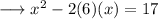
Add 6² on both sides ,

`\longrightarrow x^2-2(6)(x) + 6^2=17+6^2`

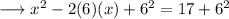
Now LHS is in the form of (a-b)² = a²-2ab+b² ; so that ;

`\longrightarrow (x -6)^2 = 17+36`

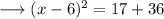
Simplify RHS ,

`\longrightarrow (x-6)^2=53`

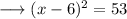
Put square root on both sides,

`\longrightarrow (x-6) = \pm√(53)`

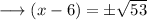
Add 6 on both sides,

`\longrightarrow x = 6\pm√(53)`

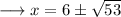
Separate the two solutions ,

`\longrightarrow \underline{\underline{x =6+√(53),6-√(53)}}`

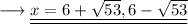
And we are done!