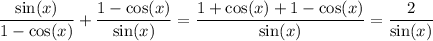(1) Recall that
sin(x - y) = sin(x) cos(y) - cos(x) sin(y)
sin²(x) + cos²(x) = 1
Given that α lies in the third quadrant, and β lies in the fourth quadrant, we expect to have
• sin(α) < 0 and cos(α) < 0
• sin(β) < 0 and cos(β) > 0
Solve for cos(α) and sin(β) :
cos(α) = -√(1 - sin²(α)) = -3/5
sin(β) = -√(1 - cos²(β)) = -5/13
Then
sin(α - β) = sin(α) cos(β) - cos(α) sin(β) = (-4/5) (12/13) - (-3/5) (-5/13)
==> sin(α - β) = -63/65
(2) In the second identity listed above, multiplying through both sides by 1/cos²(x) gives another identity,
sin²(x)/cos²(x) + cos²(x)/cos²(x) = 1/cos²(x)
==> tan²(x) + 1 = sec²(x)
Rewrite the equation as
3 sec²(x) tan(x) = 4 tan(x)
3 (tan²(x) + 1) tan(x) = 4 tan(x)
3 tan³(x) + 3 tan(x) = 4 tan(x)
3 tan³(x) - tan(x) = 0
tan(x) (3 tan²(x) - 1) = 0
Solve for x :
tan(x) = 0 or 3 tan²(x) - 1 = 0
tan(x) = 0 or tan²(x) = 1/3
tan(x) = 0 or tan(x) = ±√(1/3)
x = arctan(0) + nπ or x = arctan(1/√3) + nπ or x = arctan(-1/√3) + nπ
x = nπ or x = π/6 + nπ or x = -π/6 + nπ
where n is any integer. In the interval [0, 2π), we get the solutions
x = 0, π/6, 5π/6, π, 7π/6, 11π/6
(3) You only need to rewrite the first term:
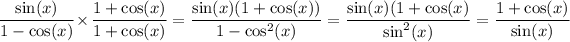
Then