Question

T=29pi/6

1. find the reference number
2. find the point on the unit circle
3. 6 trig functiond

Answer 1

the correct answer is C....I hope

Answer 2

1. **Reference Number (
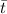`\(\bar{t}\)`):** Subtracting full revolutions,
`\(\bar{t} = (5\pi)/(6)\).`

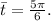
2. **Point on Unit Circle (p):** For
`\(t = (29\pi)/(6)\), \(P\left(-(√(3))/(2), -(1)/(2)\right)\).`

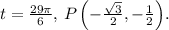
3. **Trig Functions:**

-
`\(\tan t = (√(3))/(3)\)`

-
`\(\cot t = (√(3))/(3)\)`

-
`\(\sec t = -(2√(3))/(3)\)`

-
`\(\csc t = -2\)`

-
`\(\cot t = -(√(3))/(3)\)`

-
`\(\cot t = √(3)\)`

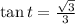
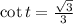
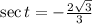
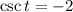
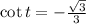
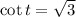
To address each part:

1. **Find the Reference Number
`\( \bar{t} \) of \( t = (29\pi)/(6) \)`:**

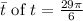- The reference angle (
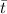`\( \bar{t} \)`) is found by subtracting full revolutions from t.

-
`\( \bar{t} = (29\pi)/(6) - 2\pi * \text{number of revolutions} \)`.

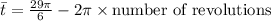- In this case,
`\( \bar{t} = (29\pi)/(6) - 2\pi * 4 = (5\pi)/(6) \).`

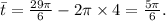
2. **Find the Point on the Unit Circle P(x, y) Determined by
`\( t = (29\pi)/(6) \)`:**

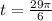- The point on the unit circle is given by
`\( P(\cos t, \sin t) \).`

-
`\( \cos (29\pi)/(6) = \cos (5\pi)/(6) = -(√(3))/(2) \).`

-
`\( \sin (29\pi)/(6) = \sin (5\pi)/(6) = -(1)/(2) \).`

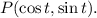
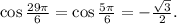
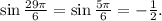
- Thus,
`\( P\left(-(√(3))/(2), -(1)/(2)\right) \).`

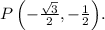
3. **The Value of All 6 Trig Functions:**

-
`\( \tan t = (\sin t)/(\cos t) = (-(1)/(2))/(-(√(3))/(2)) = (1)/(√(3)) = (√(3))/(3) \).`

-
`\( \cot t = (1)/(\tan t) = (√(3))/(3) \).`

-
`\( \sec t = (1)/(\cos t) = (1)/(-(√(3))/(2)) = -(2)/(√(3)) = -(2√(3))/(3) \).`

-
`\( \csc t = (1)/(\sin t) = -2 \).`

-
`\( \cot t = (1)/(\tan t) = -(√(3))/(3) \).`

-
`\( \cot t = (\cos t)/(\sin t) = (-(√(3))/(2))/(-(1)/(2)) = √(3) \).`

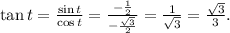
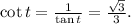
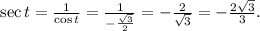
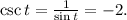
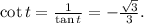
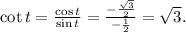
So, the reference angle is
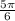`\( (5\pi)/(6) \)`, the point on the unit circle is
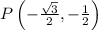`\( P\left(-(√(3))/(2), -(1)/(2)\right) \)`, and the values of all six trig functions are calculated accordingly.