Question

A loop of wire is in a magnetic field such that its axis is parallel with the field direction. Which of the following would result in an induced emf in the loop?

A. Moving the loop outside of the magnetic field region.
B. Change the diameter of the loop.
C. Change the magnitude of the magnetic field.
D. Spin the loop such that its axis does not consistently line up with the magnetic field direction.

Answer 1

All the given options will result in an induced emf in the loop.

Step-by-step explanation:

The induced emf in a conductor is directly proportional to the rate of change of flux.

`emf = -(d \phi)/(dt) \\\\where;\\\\\phi \ is \ magnetic \ flux\\\\\phi = BA\ cos \theta`

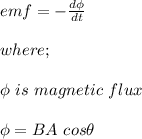
where;

A is the area of the loop

B is the strength of the magnetic field

θ is the angle between the loop and the magnetic field

Considering option A, moving the loop outside the magnetic field will change the strength of the magnetic field and consequently result in an induced emf.

Considering option B, a change in diameter of the loop, will cause a change in the magnetic flux and in turn result in an induced emf.

Option C has a similar effect with option A, thus both will result in an induced emf.

Finally, considering option D, spinning the loop such that its axis does not consistently line up with the magnetic field direction will change the angle between the loop and the magnetic field. This effect will also result in an induced emf.

Therefore, all the given options will result in an induced emf in the loop.