Answer:
The correct answer is = 15.
Explanation:
Formula:
The sum of the first n terms of an arithmetic progression with first term a and constant difference d is
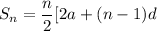
using this formula in this problem
Solution:
The sum of the first ten terms is
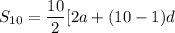
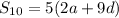
The sum of the 20th, 21st, and 22nd terms is three times the 21st term:
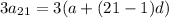
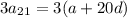
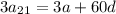
The problem then tells us
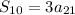
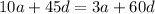
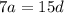
there are only positive integers and the first term a is less than 20 as given. Since 7 and 15 have no common factor, the only explanation of the requirements is a = 15 and d = 7. So the progression is
then, 15, 22, 29, 36, ...
The problem says to find the number of terms n for which the sum is 960:
putting value in the formula
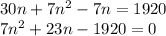
solving quadratic will give n = 15
thus, the correct answer is 15.