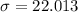Question

One invests 100 shares of IBM stocks today. He expects that there could be five possible opening prices with the respective probabilities at 9:30 a.m. in NYSE the next day. The following table lists these possible opening prices and their respective probabilities:

Outcome 1 Outcome 2 Outcome 3 Outcome 4 Outcome 5
Possible Opening
Price of IBM, Xi $182.11 $163.88 $180.30 $216.08 $144.92
Probability, pi 13% 19% 33% 17% 18%
Let X represent the five random opening prices of IBM the next day, calculate the mean, variance, and the standard deviation of X. Make your comments on the results you obtain.

Answer 1

`E(x) = 177.130`

`Var(x) = 484.551`

`\sigma = 22.013`

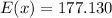
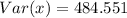
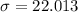
Explanation:

Given

The attached table

Solving (a): The mean

This is calculated as:

`E(x) = \sum x * p(x)`

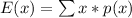
So, we have:

`E(x) = 182.11 * 13\% + 163.88 * 19\% + 180.30 * 33\% + 216.08 * 17\% + 144.92 * 18\%`

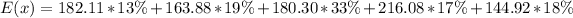
Using a calculator, we have:

`E(x) = 177.1297`

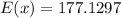
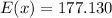`E(x) = 177.130` --- approximated

The average opening price is $177.130

Solving (b): The Variance

This is calculated as:

`Var(x) = E(x^2) - (E(x))^2`

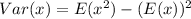
Where:

`E(x^2) = \sum x^2 * p(x)`

`E(x^2) = 182.11^2 * 13\% + 163.88^2 * 19\% + 180.30^2 * 33\% + 216.08^2 * 17\% + 144.92^2 * 18\%`

`E(x^2) = 31859.482249`

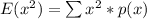
So:

`Var(x) = E(x^2) - (E(x))^2`

`Var(x) = 31859.482249 - 177.1297^2`

`Var(x) = 31859.482249 - 31374.9306221`

`Var(x) = 484.5516269`

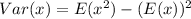
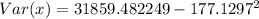
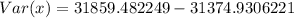
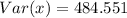`Var(x) = 484.551` --- approximated

Solving (c): standard deviation

The standard deviation is:

`\sigma = √(Var(x))`

`\sigma = √(484.5516269)`

`\sigma = 22.0125418796`

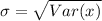
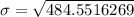
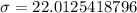
Approximate

`\sigma = 22.013`