Answer:
a)
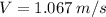
b)
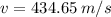
Step-by-step explanation:
a)
Using the conservation of energy between the moment when the bullet hit the block and the maximum compression of the spring.
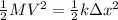
Where:
- M is the bullet-block mass (0.00535 kg + 2.174 kg = 2.17935 kg)
- V is the speed of the system
- k is the spring constant (6.17*10² N/m)
- Δx is the compression of the spring (0.0634 m)
Then, let's find the initial speed of the bullet-block system.
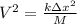

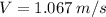
b)
Using the conservation of momentum we can find the velocity of the bullet.
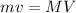
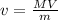

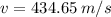
I hope it helps you!