Question

Someone please help me with this math problem?

Answer 1

D

Explanation:

5(x-5)=353 + x

the first 5 is all his tests, in the parenthesis x is the average score, and -5 is the 5 points lower mentioned in the problem.

Answer 2

B

Explanation:

We are given that Markus scored 85, 92, 82, and 94 on his first four tests and x on his fifth.

We know that his score on the fifth test is five points lower than the average of all five tests.

To find the average, we add up all the values and divide by the number of values there are. Therefore, the average of all five tests is:

`\displaystyle (85+92+82+94+x)/(5)`

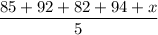
Simplify:

`\displaystyle =(353+x)/(5)`

His test score x is five points lower than the average. Hence:

`\displaystyle x=\left((353+x)/(5)\right)-5`

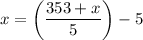
Rewrite. We can add five to both sides:

`\displaystyle x+5=(353+x)/(5)`

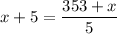
And multiply both sides by five. Hence:

`\displaystyle 5(x+5)=353+x`

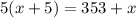
Thus, our answer is B.

Notes:

By solving the equation, we see that x = 82. So, Markus scored 82 points on his fifth test.

If that is true, then his average score of all fives tests will be:

`\displaystyle (85+92+82+94+82)/(5)=87`

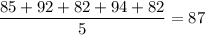
82 is indeed five points fewer than 87, so our answer is correct and matches the given information.