Question

Someone please help me with this math problem?

Answer 1

The length of the shortest side of the triangle is 10 units.

Explanation:

Let a be the shortest side of the isosceles triangle and b be the two congruent sides.

The congruent sides b are each one unit longer than the shortest side. Hence:

`b=a+1`

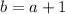
The perimeter of the isosceles triangle is given by:

`\displaystyle P_(\Delta)=b+b+a=2b+a`

This is equivalent to the perimeter of a square whose side lengths are two units shorter than the shortest side of the triangle. Let the side length of the square be s. Hence:

`s=a-2`

The perimeter of the square is:

`\displaystyle P_{\text{square}}=4s=4(a-2)`

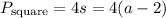
Since the two perimeters are equivalent:

`2b+a=4(a-2)`

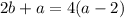
Substitute for b:

`2(a+1)+a=4(a-2)`

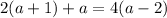
Solve for a. Distribute:

`2a+2+a=4a-8`

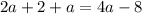
Simplify:

`3a+2=4a-8`

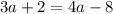
Hence:

`a=10`

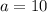
The length of the shortest side of the triangle is 10 units.