Answer:
The p-value of the test is 0.1017, which is greater than the standard significance level of 0.05, which means that this is not good evidence that the mean real compensation μ of all CEOs increased that year.
Explanation:
At the null hypothesis, we test if there was no increase, that is, the mean is 0, so:

At the alternative hypothesis, we test if there was an increase, that is, the mean is greater than 0, so:
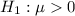
The test statistic is:

In which X is the sample mean,
 is the value tested at the null hypothesis, s is the standard deviation and n is the size of the sample.
is the value tested at the null hypothesis, s is the standard deviation and n is the size of the sample.
0 is tested at the null hypothesis:
This means that
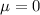
104 companies, adjusted for inflation, in a recent year. The mean increase in real compensation was x¯=6.9%, and the standard deviation of the increases was s=55%.
This means that
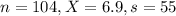
Value of the test-statistic:

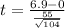
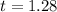
P-value of the test:
The p-value of the test is a right-tailed test(test if the mean is greater than a value), with 104 - 1 = 103 df and t = 1.28.
Using a t-distribution calculator, this p-value is of 0.1017.
The p-value of the test is 0.1017, which is greater than the standard significance level of 0.05, which means that this is not good evidence that the mean real compensation μ of all CEOs increased that year.