Question

The weights for newborn babies is approximately normally distributed with a mean of 5.4 pounds and a standard deviation of 1.8 pounds. Consider a group of 1500 newborn babies: 1. How many would you expect to weigh between 3 and 6 pounds

Answer 1

You would expect 807 babies to weigh between 3 and 6 pounds.

Explanation:

We are given that

Mean,
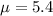`\mu=5.4`pounds

Standard deviation,
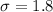`\sigma=1.8`pounds

n=1500

We have to find how many would you expect to weigh between 3 and 6 pounds.

The weights for newborn babies is approximately normally distributed.

Now,

`P(3<x<6)=P((3-5.4)/(1.8)<(x-\mu)/(\sigma)<(6-5.4)/(1.8))`

`=P(-1.33<Z<0.33)`

`P(3<x<6)=P(Z<0.33)-P(Z<-1.33)`

`P(3<x<6)=0.62930-0.09176`

`P(3<x<6)=0.538`

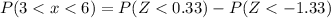
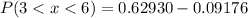
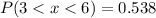
Number of newborn babies expect to weigh between 3 and 6 pounds

=
`1500* 0.538=807`