Given:
The focus of the parabola is at (6,-4).
Directrix at y=-7.
To find:
The equation of the parabola.
Solution:
The general equation of a parabola is:
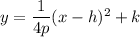 ...(i)
...(i)
Where, (h,k) is vertex, (h,k+p) is the focus and y=k-p is the directrix.
The focus of the parabola is at (6,-4).
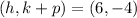
On comparing both sides, we get
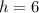
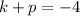 ...(ii)
...(ii)
Directrix at y=-7. So,
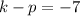 ...(iii)
...(iii)
Adding (ii) and (iii), we get
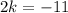
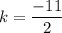

Putting
 in (ii), we get
in (ii), we get
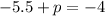
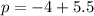
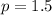
Putting
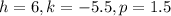 in (i), we get
in (i), we get
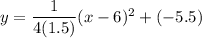
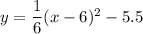
Therefore, the equation of the parabola is
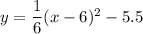 .
.