Question

For the geometric series 2 + 6 + 18 + 54 + ... , find S8

Answer 1

S₈ = 6560

Explanation:

The sum to n terms of a geometric sequence is

`S_(n)` =
`(a(r^(n)-1) )/(r-1)`

where a is the first term and r the common ratio

Here a = 2 and r =
`(a_(2) )/(a_(1) )` =
`(6)/(2)` = 3 , then

S₈ =
`(2(3^(8)-1) )/(3-1)`

=
`(2(6561-1))/(2)`

= 6561 - 1

= 6560

Answer 2

`\displaystyle S_(8)=6560`

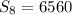
Explanation:

We have the geometric sequence:

2, 6, 18, 54 ...

And we want to find S8, or the sum of the first eight terms.

The sum of a geometric series is given by:

`\displaystyle S=(a(r^n-1))/(r-1)`

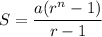
Where n is the number of terms, a is the first term, and r is the common ratio.

From our sequence, we can see that the first term a is 2.

The common ratio is 3 as each subsequent term is thrice the previous term.

And the number of terms n is 8.

Substitute:

`\displaystyle S_8=(2((3)^(8)-1))/((3)-1)`

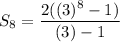
And evaluate. Hence:

`\displaystyle S_8=6560`

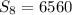
The sum of the first eight terms is 6560.