Question

Julie drives 100 mi to Grandmother's house. On the way to Grandmother's, Julie drives half the distance at 40.0 mph and half the distance at 60.0 mph . On her return trip, she drives half the time at 40.0 mph and half the time at 60.0 mph.

Required:
a. What is Julie's average speed on the way to grandmother's house?
b. What is her average speed in the return trip?

Answer 1

a. The average speed on her way to Grandmother's house is 48.08 mph

b. The average speed in the return trip is 50 mph.

Step-by-step explanation:

The average speed (S) can be calculated as follows:

`S = (D)/(T)`

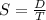
Where:

D: is the total distance

T: is the total time

a. To find the total distance in her way to Grandmother's house, we need to find the total time:

`T_(i) = t_{1_(i)} + t_{2_(i)} = \frac{d_{1_(i)}}{v_{1_(i)}} + \frac{d_{2_(i)}}{v_{2_(i)}}`

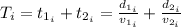
Where v is for velocity

`T = \frac{d_{1_(i)}}{v_{1_(i)}} + \frac{d_{2_(i)}}{v_{2_(i)}} = ((100/2) mi)/(40.0 mph) + ((100/2) mi)/(60.0 mph) = 1.25 h + 0.83 h = 2.08`

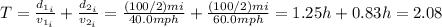
Hence, the average speed on her way to Grandmother's house is:

`S_(i) = (D)/(T_(i)) = (100 mi)/(2.08 h) = 48.08 mph`

b. Now, to calculate the average speed of the return trip we need to calculate the total time:

`D = v_{1_(f)}(T_(f))/(2) + v_{2_(f)}(T_(f))/(2) = (T_(f))/(2)(v_{1_(f)} + v_{2_(f)})`

`100 mi = (T_(f))/(2)(40 mph + 60 mph)`

`T_(f) = (200 mi)/(40 mph + 60 mph) = 2 h`

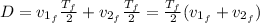
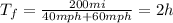
Therefore, the average speed of the return trip is:

`S_(f) = (D)/(T_(f)) = (100 mi)/(2 h) = 50 mph`

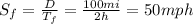
I hope it helps you!