Question

The random variable is the number of houses sold by a realtor in a single month at the Sendsom's Real Estate Office. Its probability distribution is as follows. Find the standard deviation for the probability distribution.

Houses sold(x): 0 1 2 3 4 5 6 7
Probability (P(X)): 0.24 0.01 0.12 0.16 0.01 0.14 0.11 0.21

Answer 1

The standard deviation for the probability distribution is of 2.63 houses sold.

Explanation:

To find the standard deviation for the distribution, first we have to find the mean.

Mean:

Each outcome multiplied by it's probability. So

`E(X) = 0.24*0 + 0.01*1 + 0.13*2 + 0.16*3 + 0.01*4 + 0.14*5 + 0.11*6 + 0.21*7 = 3.62`

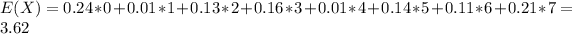
Standard deviation:

Square root of the sum of the differences squared between each value and the mean, multiplied by its probabilities. So

`√(V(X)) = √(0.24(0-3.62)^2 + 0.01(1-3.62)^2 + 0.13(2-3.62)^2 + 0.16(3-3.62)^2 + ...) = 2.63`

The standard deviation for the probability distribution is of 2.63 houses sold.