Question

Find the slope of a line parallel to a line that contains the points (9, -3) and (-3, 8).

Answer 1

`Slope, \ m = \frac {11}{-12}`

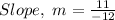
Step-by-step explanation:

Given the following points;

Points on the x-axis (x1, x2) = (9, -3)

Points on the y-axis (y1, y2) = (-3, 8)

To find the slope of a line parallel to a line;

Mathematically, the slope of a line is given by the formula;

`Slope, \ m = \frac {Change \; in \; y-axis}{Change \; in \; x-axis}`

`Slope, \ m = \frac {y_(2) - y_(1)}{x_(2) - x_(1)}`

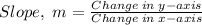
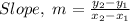
Substituting into the formula, we have;

`Slope, \ m = \frac {8 - (-3)}{-3 - 9}`

`Slope, \ m = \frac {8 + 3}{-3 - 9}`

`Slope, \ m = \frac {11}{-12}`

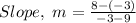
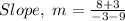
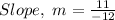
Therefore, the slope of the parallel line is -11/12.