Question

Let F(x) = x^2 – 15 and
G(x)= 4 - x
Find (F/G)(–7) =

Answer 1

`\displaystyle \bigg( (F)/(G) \bigg)(-7) = (34)/(11)`

General Formulas and Concepts:

Pre-Algebra

Order of Operations: BPEMDAS

1. Brackets
2. Parenthesis
3. Exponents
4. Multiplication
5. Division
6. Addition
7. Subtraction

• Left to Right

Algebra I

• Functions
• Function Notation

Explanation:

Step 1: Define

Identify

F(x) = x² - 15

G(x) = 4 - x

Step 2: Find

1. Substitute in functions:
   `\displaystyle \bigg( (F)/(G) \bigg)(x) = (x^2 - 15)/(4 - x)`

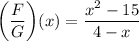
Step 3: Evaluate

1. Substitute in x [Function (F/G)(x)]:
   `\displaystyle \bigg( (F)/(G) \bigg)(-7) = ((-7)^2 - 15)/(4 - (-7))`
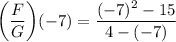
2. Exponents:
   `\displaystyle \bigg( (F)/(G) \bigg)(-7) = (49 - 15)/(4 - (-7))`
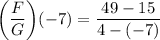
3. Subtract:
   `\displaystyle \bigg( (F)/(G) \bigg)(-7) = (34)/(11)`