Answer:
see below
Explanation:
given function:
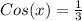
- ------------------------------------------------------------------------------------------------------
Cosine - (In a right triangle, the ratio of the length of the adjacent side to the length of the hypotenuse.)
- ---------------------------------------------------------------------------------------------------
#1: Take the inverse cosine of both sides of the equation to extract
 from inside the cosine.
from inside the cosine.

#2: Evaluate
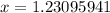
#3: The cosine function is positive in the first and fourth quadrants. To find the second solution, subtract the reference angle from
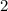 π to find the solution in the fourth quadrant.
π to find the solution in the fourth quadrant.
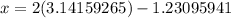
#4: Simplify the equation above.
- Multiply
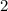 by
by

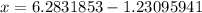
- Subtract
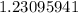 from
from


#5: Find the period.
- The period of the function can be calculated using
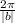 .
.
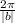
- Replace
 with
with
 in the formula for period.
in the formula for period.
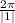
#6: Solve the equation.
- The absolute value is the distance between a number and zero. The distance between
 and
and
 is
is
 .
.
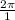
- Divide
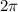 by
by
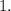
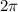
The period of the
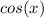 function is
function is
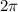 so values will repeat every
so values will repeat every
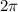 radians in both directions.
radians in both directions.
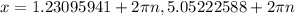 , for any integer
, for any integer
